Strange Attractors GPU

Attractors have been out for a while and as it happens in these cases there’re a lot of resources on the internet involving this subject. They are marvellous mathematical objects pretty easy to program that give rise to interesting elegant outcomes. For a deeper understading of what an attractor is I suggest a quick look to the wiki page and the Softology’s blog page.

The visualization of a strange attractor displays the phase space of a chaotic dynamical system. They are defined by a set of differential equations solved by approximating the system of equations using something like the Euler’s method or the Runge-Kutta method. To put it simply I used a particle system with starting random position for every element in the simulation and calculate the next position with a set of simple iterated functions that gives the next particle’s position.

The easiest way I found to implement the strange attractors was to do all the calculation inside a fragment shader that take care of defining the particle’s position.

Here’s an example of a fragment shader that calculates the particle’s motion while affected by Lorenz attractor.

#version 330

// ping pong inputs
uniform sampler2DRect particles0;
uniform sampler2DRect particles1;

uniform float timestep;

in vec2 texCoordVarying;

layout(location = 0) out vec4 posOut;
layout(location = 1) out vec4 velOut;


// Lorenz Attractor parameters
float a = 10.0;
float b = 28.0;
float c = 2.6666666667;


void main()
{
    
    int id = int(texCoordVarying.s) + int(texCoordVarying.t)*int(textureSize(particles0).x);
    vec3 pos = texture(particles0, texCoordVarying.st).xyz;
    vec3 vel = texture(particles1, texCoordVarying.st).xyz;

    // Previous positions
    float x = pos.x;
    float y = pos.y;
    float z = pos.z;
    
   	// Increments calculation
    float dx = (a * (y - x))   * timestep;
    float dy = (x * (b-z) - y) * timestep;
    float dz = (x*y - c*z)     * timestep;
    
	// Add the new increments to the previous position
    vec3 attractorForce = vec3(dx, dy, dz) ;
    pos +=attractorForce;

    
    
    posOut = vec4(pos, id);
    velOut = vec4(vel, 0.0);
}

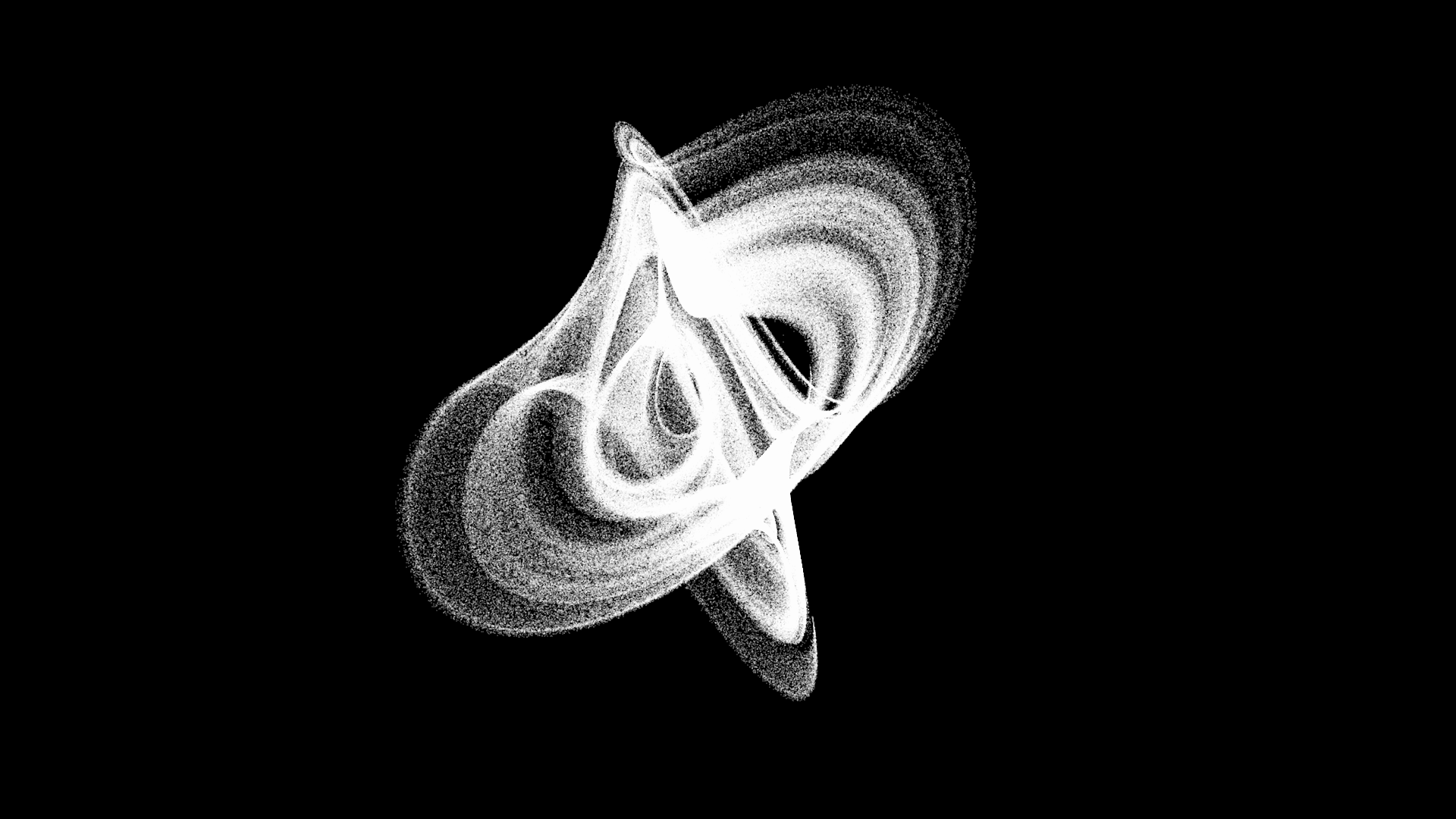
Down here a few more examples of attractors and their relative set of differential equations.

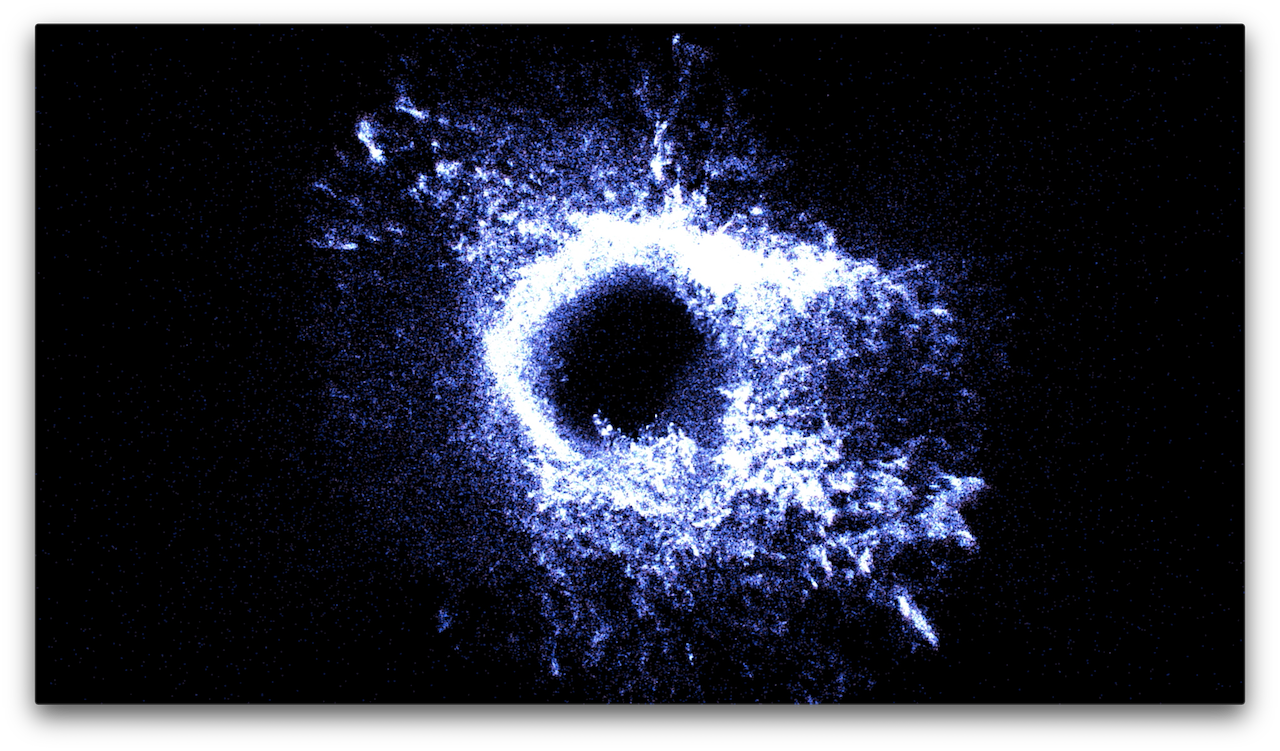
Aizawa Attractor

Attractor parameters

float a = 0.95;
float b = 0.7;
float c = 0.6;
float d = 3.5;
float e = 0.25;
float f = 0.1;
        
dx = ((z-b) * x - d*y) * timestep;
dy = (d * x + (z-b) * y) *timestep;
dz = (c + a*z - ((z*z*z) /3) - (x*x) + f * z * (x*x*x)) * timestep;

Arneodo Attractor

Attractor parameters

float a = -5.5;
float b = 3.5;
float d = -1;
        
dx = y * timestep;
dy = z * timestep;
dz = (-a*x -b*y -z + (d* (pow(x, 3)))) * timestep;

Dadras Attractor

Attractor parameters

float a = 3;
float b = 2.7;
float c = 1.7;
float d = 2;
float e = 9;
        
dx = (y- a*x +b*y*z) * timestep;
dy = (c*y -x*z +z) * timestep;
dz = (d*x*y - e*z) * timestep;

Dequan Attractor

Attractor parameters

float a = 40.0;
float b = 1.833;
float c = 0.16;
float d = 0.65;
float e = 55.0;
float f = 20.0;
        
dx = ( a*(y-x) + c*x*z) * timestep;
dy = (e*x + f*y - x*z) * timestep;
dz = (b*z + x*y - d*x*x) * timestep;

Lorenz Attractor

Attractor parameters

float a = 10.0;
float b = 28.0;
float c = 2.6666666667;
        
dx = (a * (y - x)) * timestep;
dy = (x * (b-z) - y) * timestep;
dz = (x*y - c*z) * timestep;

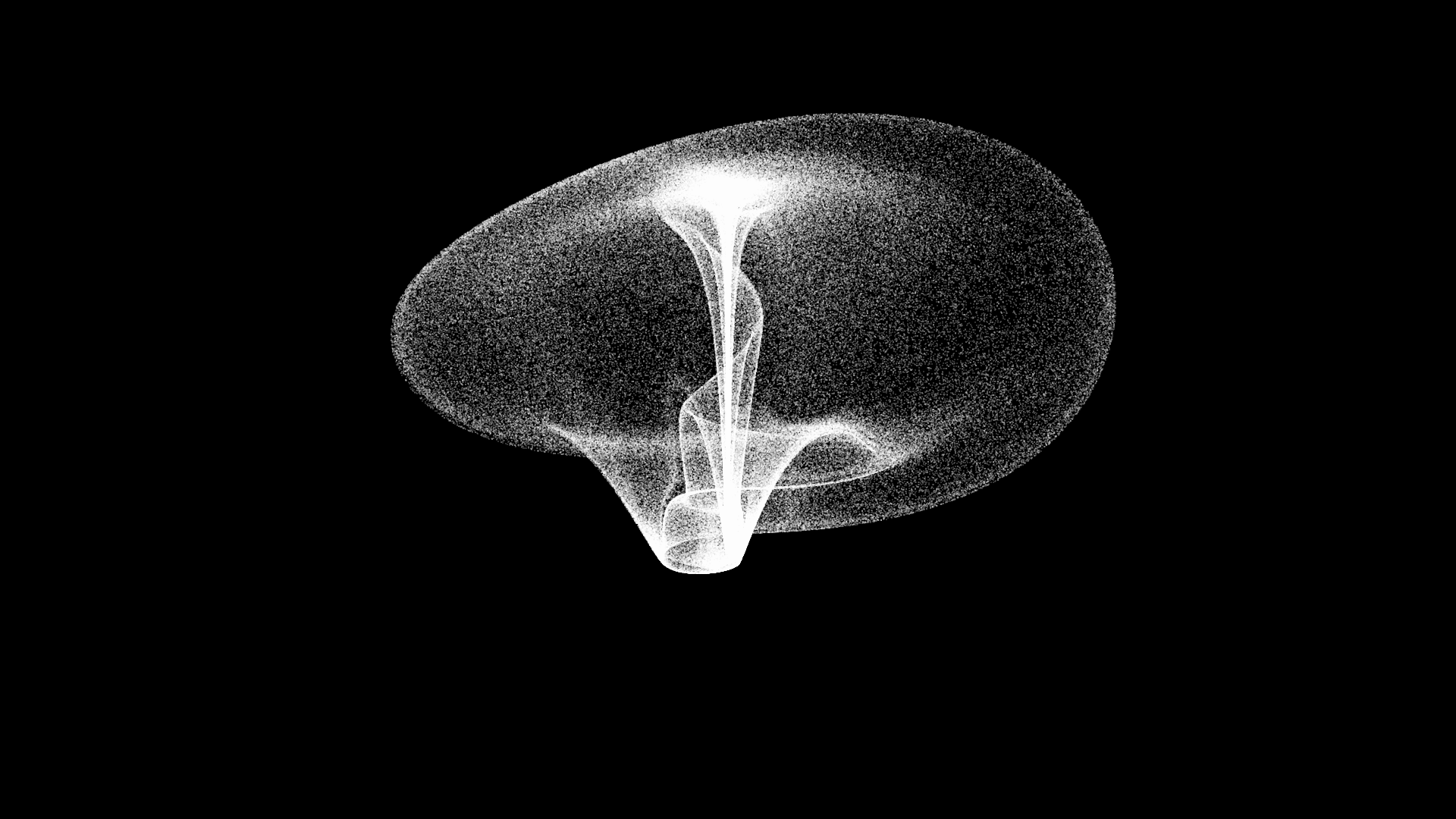
Lorenz Mod 2 Attractor

Attractor parameters

float a = 0.9;
float b = 5.0;
float c = 9.9;
float d = 1.0;
        
dx = (-a*x+ y*y - z*z + a *c) * timestep;
dy = (x*(y-b*z)+d)  * timestep;
dz = (-z + x*(b*y +z))  * timestep;

Thomas Attractor

Attractor parameters

float b = 0.19;

dx = (-b*x + sin(y)) * timestep;
dy = (-b*y + sin(z)) * timestep;
dz = (-b*z + sin(x)) * timestep;

Three-Scroll Unified Chaotic System Attractor 1

Attractor parameters

float a = 40.0;
float b = 0.833;
float c = 20.0;
float d = 0.5;
float e = 0.65;
       
 dx = (a*(y-x) + d*x*z)   * timestep * 0.1 ;
 dy = (c*y - x*z )        * timestep * 0.1 ;
 dz = (b*z + x*y - e*x*x) * timestep * 0.1 ;